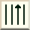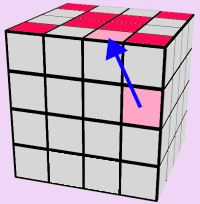
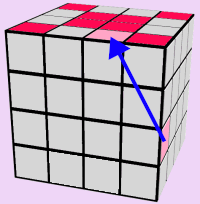
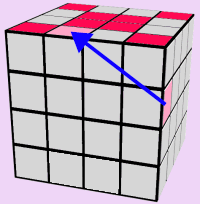
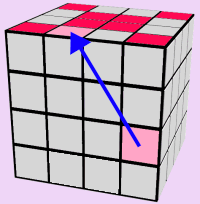
Denny's solution for solving the Rubik's Revenge (4x4x4 cube)

• Terminology
• Top Corners
• Top Centers
• Bottom Corners
• Bottom Centers
• Top and Bottom Edges
• Side Edges
• Side Centers

TOP/BOTTOM EDGES: RED FACE

Let's start by completing the Red Edges. The premise for this step is to find and move all appropriate edges, from the two center rows, up onto the Red Side of the cube.

Use the 5 images below to assist you in solving the entire Red Face of the cube. If you run out of pieces on the two center rows:

1. You will most likely find more on the bottom layer. If so, the fifth step below will move bottom pieces up into the two center rows so that you can use steps 1 through 4 to properly place the pieces.
2. It is also possible that all the Red Edges are actually on the top but in the wrong positions. If so, use one of the steps (1-4) to put a bogus piece in it's place, thus forcing it out of the top position.

STEP 1
STEP 2
STEP 3
STEP 4
STEP 5

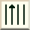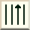
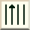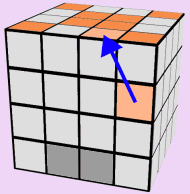
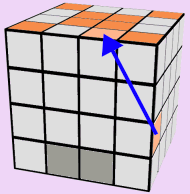
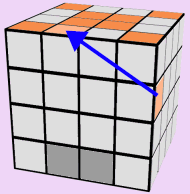
ORANGE FACE:

Now that the Red Face of the cube is finished, lets flip the cube over and finish the Orange Side.

Unfortunately fixing the Orange Side will actually temporarily mess up two of your completed Red Edges that you just finished placing. That's okay though, because we will soon put them back.

When you used steps 1 - 4 above the process successfully moved your piece into place, but it had another, probably unnoticed effect. It actually messed up the pieces in the Dark Gray positions (see images below). We didn't really care before, since we were not concerned with the Orange Edges yet.

We need to sacrifice a pair of finished Red Edges. This will allow us to finish the entire Orange side of the cube at which time we will put the Red Pair back in place.

Use the 5 images below to assist you in solving the entire Orange Face of the cube. If you run out of pieces on the two center rows:

1. You may find that one of the pieces in the Gray Positions need to be placed on the Orange Side. If so, the fifth step below will move bottom Gray pieces up into the two center rows so that you can use steps 1 through 4 to properly place the pieces.
2. It is also possible that all the Orange Edges are actually on the Orange Face but in the wrong positions. If so, use one of the steps (1-4) to put a bogus piece in it's place, thus forcing the Orange piece out of the top position.

• Each time you perform a move, ensure the sacrificed pair are in the Front Bottom position.

STEP 1
STEP 2
STEP 3
STEP 4
STEP 5

THOSE TWO GRAY PIECES

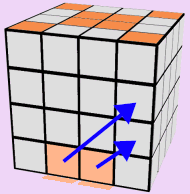
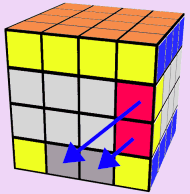
Finally, the Orange side is now complete, and the Red Side is missing two Edges. One more step and we can put those two Red Pieces in place.

If you find that the two remaining Red Edges are in BOTH the Second and Third Layer, match your cube to the samples in Step 1 and Step 2 and follow the appropriate step to finish the Red Side. Again, the colors shown are not relevant, just the move itself is important.

• If the two remaining Red Edges are on the Same Layer you will need to use another procedure first.
• If one or two of the Red Edges are actually on the Bottom Layer (in the gray positions) then you will need to perform another step first.

STEP 1
STEP 2

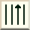
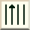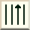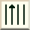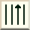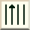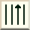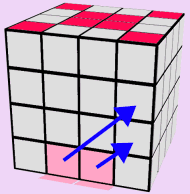
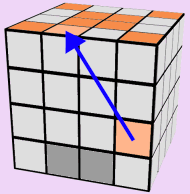
LAST TWO RED EDGES ARE ON THE SAME LAYER

Our goal here is to move the last two Red Edges onto two separate layers. Position one of the Red/Yellow Edges on the Left Side of the Face of the cube so that the other Red/Yellow Edge is in one of the two light-red positions as shown. Match your cube up to the following two scenarios and perform whichever process needs completing.

STEP 1
STEP 2

A RED EDGE IS ALREADY ON THE BOTTOM

• If both pieces are already on the bottom but the colors are flipped, perform the step below.
• If one is on the Second or Third layer but the other is on the Bottom, spin the Second or Third layer until the piece is on the Back side of the cube, and then perform this step below.

Back to Matt Monroe's Cube solution pages