Isotopic Calculations

The Mathematics behind the Isotopic Extremes error handler

When a user types in an isotopic mass (eg. ^{^13}C for carbon-13), the program checks to see if the isotope is a reasonable value. Obviously, ^{^5}C (carbon-5) would be unreasonable because any compound with 6 protons (i.e. carbon) must have a minimum weight of 6. However, upon examining the Table of Isotopes in the CRC Handbook of Chemistry and Physics, I found that very few compounds have zero neutrons (and thus an atomic weight equal to the number of protons in the element). Therefore, I examined the table and used MS Excel to create a graph of the highest and lowest isotopic masses for every element (shown below). I then determined two fit-lines that encompassed all the data points -- one for the upper extreme and one for the lower extreme.

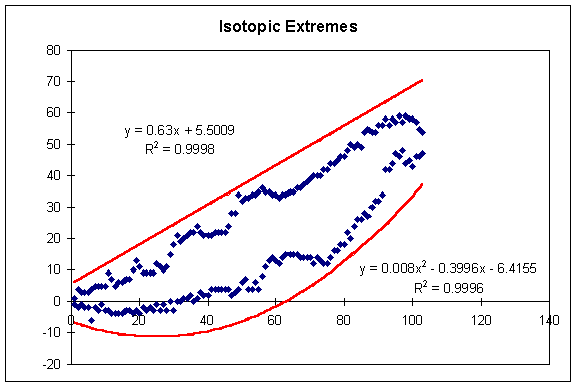
Since most isotopic masses occur somewhere around the value twice the atomic number (Z) of the element, I chose to work with the value:

x = isotope_value - Z*2

where isotope_value is the value present after the caret (^) in the formula.

The curve that describes the upper limit of these x values is:

max_x = INTEGER(0.63*Z + 6)

where max_x is the maximum allowable x value before a warning is issued.

The curve that describes the lower limit of these x values is:

min_x = INTEGER(0.008*Z² - 0.4*Z - 6)

where min_x is the minimum allowable x value before a warning is issued. The results were converted to integers to aid in program design.

Finally, because the min_x value is too low for some of the lighter elements, I included a test to make sure that isotope_value was at least as large as Z, or else a warning was again issued to the user. The method is an approximate test on the isotope value, and is designed to catch the outrageous isotopic masses. It does not catch the borderline ones since that would have increased the program size and memory usage by too much.

Examples:

For Carbon:

^{^13}C has z = 6, x = 1, max_x = 9 and min_x = -9

Because x < 9 and x > -9 and x > 6, no warning is issued.

(The average atomic weight of carbon is 12.011)

^{^25}C has z = 6, x = 10, max_x = 9 and min_x = -9

Because x > 9, a warning that 25 is probably too large is given.

In reality, the heaviest known carbon isotope is carbon-16.

^{^5}C has z = 6, x = -7, max_x = 9 and min_x = -9

Although x < 9 and x > -9, x is less than 6 so a warning is again issued.

In reality, the lightest known carbon isotope is carbon-9.

For Silver:

^{^100}Ag has z = 47, x = 6, max_x = 35 and min_x = -8

Because x < 35 and x > -8 and x > 47, no warning is issued.

(The average atomic weight of silver is 107.87)

^{^130}Ag has z = 47, x = 36, max_x = 35 and min_x = -8

Because x > 35, a warning that 130 is probably too large is given.

In reality, the heaviest known silver isotope is silver-122.

^{^85}Ag has z = 47, x = -9, max_x = 35 and min_x = -8

Because x < -8 a warning that 85 is probably too small is given.

In reality, the lightest known silver isotope is carbon-96.

The above calculations show, as mentioned above, that this method catches the outrageous isotopic masses but does not catch the borderline cases. Furthermore, it should also be evident that this method is more accurate for the heavier elements, a consequence of the unusual isotopic behavior of the lighter elements.

Back to the Molecular Weight Calculator download page